I received an email the other day from two consulting engineers in North Carolina.  The engineers, let’s call them R and G, wanted me to resolve their dispute regarding ‘Head’ vs “Pressure’ in the interpretation of pump performance curves. 

R was satisfied that pump performance curves plot head and flow. G thought all pump curves should plot differential pressure (psid) and flow. He reasoned that new pumps are verified on a test stand using differential pressure, which is then converted to feet of water for the published pump curve. G thought ‘feet-of-head’ was a misleading conversion because different liquids have different densities. He thought the curve should report differential pressure of the actual liquid, with its unique specific gravity. The specific gravity is the liquid’s density, or weight relative to an equal volume of water.  

This dispute reveals the disparity in the education and experience of these two engineers.  Portions of G’s rationale are correct.  

For simplicity and practicality, most pump companies develop the performance curve of a new pump by installing the pump into a pipe loop with a holding tank of ambient water.  The test engineer records the differential pressures across the pump at various flows controlled with a valve. Later, the differential pressures are converted to feet (or meters) of head in the published performance curve.

What is neither simple nor practical is to stretch a length of pipe 800-ft. into the sky just to verify a pump that develops 800 ft. of head. Head converts easily to differential pressure, and differential pressure converts easily to head. It is easy to measure differential pressure in a loop at ground level, and then convert to head.

Also, pumps are tested on ambient water. A test stand might have a tank of 2,000 or 5,000 gallons of water.  The pump company won’t dump the water and fill the tank with soy sauce, vodka, sulfuric acid, or coffee liquor just to verify the differential pressure across a pump with a particular liquid. If the purchaser supplies the liquid’s specific gravity, viscosity, temperature and the pump’s elevation above sea level, the pump company will supply a certified curve adjusted to the properties of the actual liquid.   

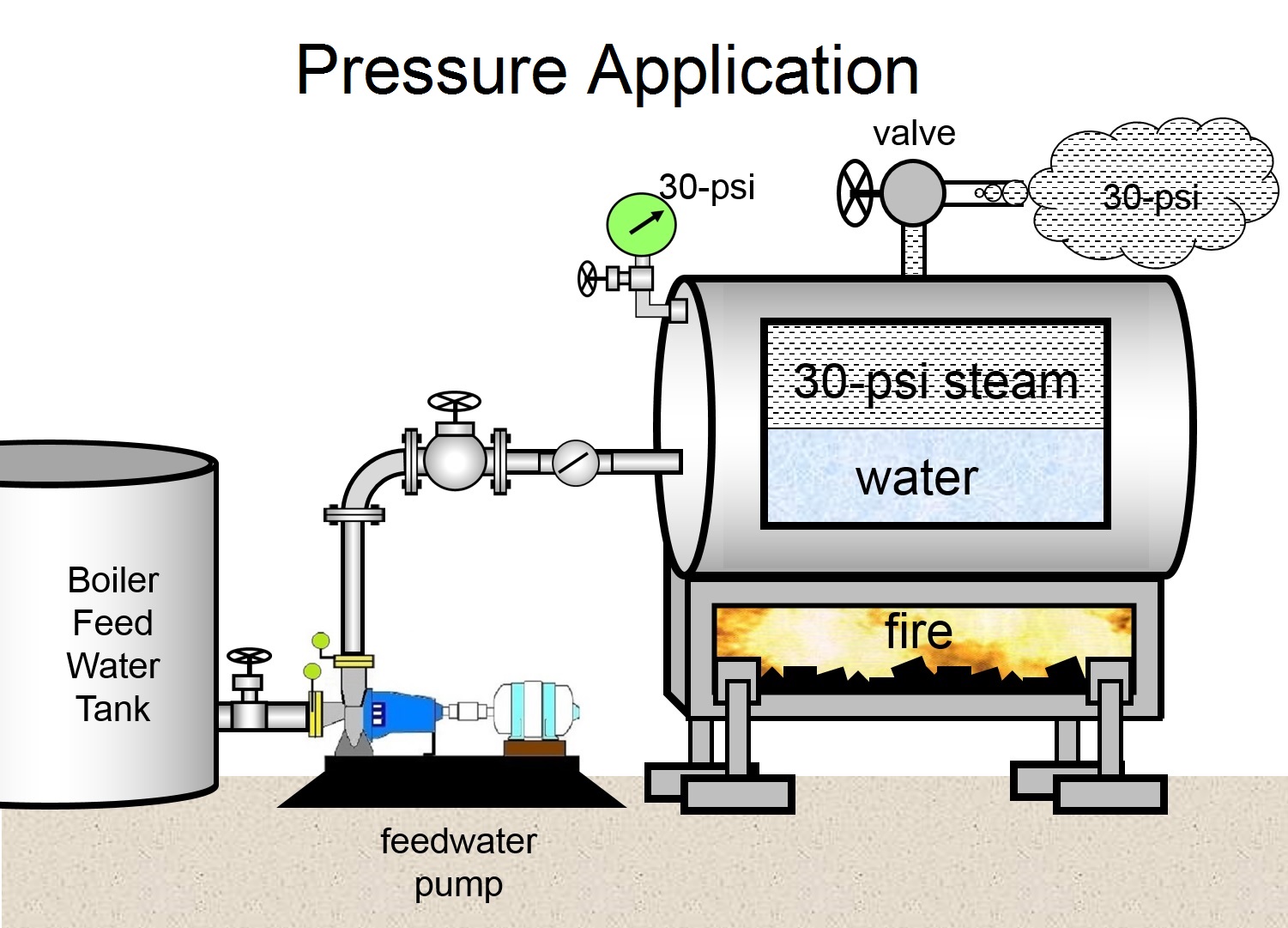
There are some applications in industry where a pump is specified by pressure.  For example, if the pressure in a steam boiler is 20-psi, then the discharge pressure of the boiler feedwater pump must be at or slightly above 20-psi to push more water into the boiler.

Diagram shows a pump developing head

There are more industrial applications where the pump is specified to elevate a liquid.  For example, let’s say an industrial tank rises 40 feet above a pump, and you want to use the pump to fill the tank.  The pump should develop 40-ft of head to fill this tank.

At this point, G’s rationale goes askew, and R’s opinion is correct.  A pump, designed to develop 40-ft of head, will elevate cold water 40-ft. The same pump will elevate gasoline 40-ft.  The same pump will elevate sulfuric acid 40-ft. We don’t care about the name of the liquid or its specific gravity. What we need is 40-ft.  These applications abound in the chemical process industry.

Cold water, gasoline, and sulfuric acid each have a unique specific gravity.  I don’t need the specific gravity if the pump is rated in feet (or meters) of head. I need the liquid’s specific gravity if I want to convert feet of head into pressure.  

By definition, ‘Head’ is a measure of energy.  The units of energy are feet (or meters). ‘Pressure’ is a force applied against a unit of area such as a pound of force applied to a square inch of area (psi).  The liquid’s density determines the force. 

Rating a pump by ‘feet-of-head’ is the standard in the pump industry for a few reasons.  One reason is because there are many applications where the pump is specified to elevate the liquid.  Another reason is because the liquid’s density is not a component of ‘head’. The density is a component of pressure. 

There is another reason rooted in history. About 2,400-years ago, the Greek Philosopher Aristotle proposed that gravitational attraction was a function of an object’s mass.  In simple terms, Aristotle said a 10-lb. rock will free-fall to earth twice as fast as a 5-lb. rock. A 10-lb. ball will free-fall to earth ten times as fast as a 1-lb. ball. It seemed logical at the time.  There were no helicopters, sky cranes or tall buildings in those days.  There was no practical way to prove or disprove Aristotle’s theory. Aristotle’s theory was unchallenged for 2,000 years.  

Then in 1589, the Italian engineer/astronomer/physicist Galileo carried two objects of different weights to the top of the Leaning Tower of Pisa in Italy.  The Leaning Tower is almost 200-ft high. Galileo released the objects together. The two objects fell together to Earth and struck the ground at the same instant. Galileo proclaimed that gravitational attraction is a constant, independent of the object’s mass or weight.

Galileo continued experimenting and determined that the acceleration of gravity is also a constant. All objects accelerate toward the Earth in a free fall at 32.16-ft./sec2 (9.8-m./sec2).  These values appear frequently in formulas as engineering students study Fluid Mechanics in university. 

Therefore, if the acceleration of gravity is a constant, then accelerating an object against gravity is also a constant.  Launching a rocket into space conforms to Galileo’s theory. And elevating a gallon of water, or a gallon of house paint, or a gallon of orange juice is also a constant.

What does this mean for pumps that elevate liquids?  It means that a pump performance curve, rated in feet or meters of head, applies to all liquids.  If I use the term ‘feet’ (or meters) of head when discussing pumps, the liquid’s density doesn’t really matter.  If I discuss pumps using pressure (psi), the liquid’s specific gravity is a component of pressure.

I know what you’re thinking.  Even if gravity is a constant, there MUST be some observable difference between dropping two objects of different weights from a high elevation, or elevating two different liquids in a pipe.  Yes, there is a difference. Let’s go back to Galileo and the Leaning Tower of Pisa.    

Equally important but rarely mentioned in the history books is the fact that the heavier object required proportionally more effort to carry to the top of the Leaning Tower compared to the lighter object.  And, the heavier object left a proportionally larger/deeper crater in the ground at the point of impact.  

It means the horsepower, or kilowatts, must be multiplied by the liquid’s specific gravity.  The power rating (BHp or kW) on most standard pump curves is based on water with a specific gravity of 1.0. 

The Hammer and the Feather

Galileo made great strides in our understanding of planetary gravity, the solar system and modern engineering.  However, when questioned in 1589, Galileo couldn’t explain, “If gravity is a constant, then why does it take so long for a feather, or a leaf falling from a tree, to reach the ground?” 

In 1589, there was no concept of atmospheric pressure, air pressure, air currents or air friction.  Galileo couldn’t explain that the air interfered with a feather’s free-fall to Earth by gravity. These concepts were explored and explained a century or so later by Isaac Newton, Blaise Pascal, and Daniel Bernoulli. 

In 1971, the astronauts of Apollo 15 finally answered the question put before Galileo back in 1589.  Go to ‘You Tube’ and enter “Apollo 15 Hammer and Feather Experiment”.  You will see the video of what happens when a feather and a hammer are dropped together in the absence of air on the moon.

I hope this answers the question of ‘head’ vs ‘pressure’. If you have any questions about pumps, please post your inquiries in the comments section!

About Larry Bachus

Many people call Larry ‘The Pump Guy’. Larry writes the ‘Pump Guy’ column in Flow Control Magazine, World Pumps Magazine, Mechanical Technology Magazine and to some 40,000 monthly newsletter subscribers. A few of The Pump Guy articles are available on our articles page. Larry writes like he talks. If you like the articles, you will love his books “Know and Understand Centrifugal Pumps” and “Centrifugal Pumps and Everything You Need to Know About Pumps” written in both English and Spanish versions (“Bombas Centrífugas, y Todo lo que Necesita Saber Sobre Ellas”). Larry continues inventing products when not lecturing and consulting. As a member of ASME (American Society of Mechanical Engineers), most of Larry’s products find application in civil and mechanical engineering.